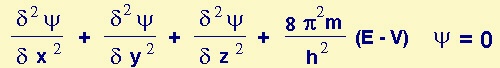L'atomo di idrogeno, sulla base dei dati sperimentali, possiede:

- un nucleo con una carica positiva e quasi tutta la massa dell'atomo

- un elettrone con una carica negativa e che si muove attorno al nucleo

Nucleo ed elettrone interagiscono elettrostaticamente; l'energia totale E_tot del sistema è costituita da due componenti, energia potenziale E_pot ed energia cinetica E_cin

E_pot è l'energia dovuta alla mutua posizione nucleo-elettrone in ogni istante;

E_cin è l'energia dovuta al movimento dell'elettrone.

E_tot, in assenza di perturbazioni (dovute ad acquisto o perdita di energia da parte del sistema), è costante e corrisponde a quella dell'atomo nello stato fondamentale (n=1) a più bassa E.

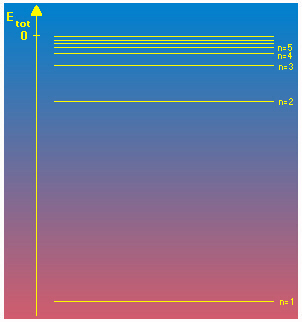
Fig.6.1 Modello dei livelli energetici dell'elettrone di un atomo di idrogeno. Per assorbimento di E quantizzata l'atomo può passare agli stati eccitati (che hanno cioè n > 1) ; poi in 10-12 s, per emissione di E quantizzata, può tornare a n = 1. Stati stazionari sono il complesso totale di stati, cioè il fondamentale più quelli eccitati (cioè, praticamente la loro sommatoria Si ni) Emax = 0 rappresenta il limite corrispondente alla ionizzazione: in questa situazione infatti Epot = 0, (l'elettrone è "infinitamente" lontano dal nucleo, perciò non esiste alcuna interazione tra loro) Ecin = 0 (l'elettrone è "fermo", gli viene cioè data l'energia per allontanarlo dal nucleo fino a distanza "infinita", ma nulla di più che gli permetta di muoversi; questo "di più" sarebbe energia continua e non più quantizzata).

Nel modello energetico l'energia E viene intesa come negativa, poiché la consideriamo come una E di stabilizzazione.

Per descrivere il comportamento dell'elettrone attorno all'atomo possono essere utili delle funzioni matematiche che tengano conto del campo di potenziale in cui si trova l'elettrone; ma il campo è condizionato dalla posizione istantanea dell'elettrone rispetto al nucleo e questa è rappresentabile con un sistema di coordinate cartesiane in cui l'origine degli assi coincide con il centro del nucleo M.

Fig.6.2 Posizione dell'elettrone e rispetto alle tre coordinate cartesiane la cui origine è costituita dal nucleo dell'atomo M.     La posizione dell'elettrone, rispetto a questo sistema di riferimento, è definita, in ogni istante, da una terna di valori (xi, yi, zi). Una rappresentazione perfettamente equivalente dal punto di vista operativo può essere ottenuta anche mediante coordinate polari.

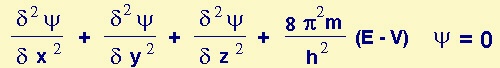
Fig.6.3 Erwin Schrödinger   Nel 1926 Erwin Schrödinger (1887-1961; premio Nobel nel 1933) sviluppò una equazione differenziale la cui soluzione è la funzione desiderata, cioè quella che rappresenta la posizione dell'elettrone rispetto alla sua energia; questa funzione y è chiamata funzione d'onda. L'equazione differenziale é: in cui:

(d²y / dx²), (d²y / dy²), (d²y / dz²) sono le derivate seconde parziali della funzione y rispetto alle direzioni x, y e z;

m è la massa dell'elettrone;

E è l'energia totale dell'elettrone (E_tot);

V è l'energia potenziale dell'elettrone (E_pot);

y è la funzione d'onda

E' evidente che il termine (E-V) rappresenta l'energia cinetica (E_cin)

Sia E sia y sono incognite; trattandosi perciò di una equazione a due incognite, esisteranno infinite soluzioni dell'equazione: ad un certo valore per l'energia (detto autovalore) E_i, corrisponderà una certa funzione y_i (detta autofunzione).

Potremo perciò conoscere l'energia dell'elettrone in funzione dei suoi spostamenti (in effetti la cosa è più complessa, ma in prima approssimazione questo può essere sufficiente).

Queste y, per gli atomi, possiamo chiamarle orbitali. Ad ogni stato stazionario corrisponde una y_i e perciò una ben determinata E_i.

Le varie y possono avere, tra l'altro, anche "forme" speciali diverse. Ciò dipende da parametri che sono chiamati numeri quantici.