E' un tipo di legame che può instaurarsi solo tra atomi diversi.

Sappiamo che molti atomi possono diventare ioni, per acquisto o perdita di elettroni: alcuni, che hanno bassa energia di ionizzazione, possono dare facilmente cationi, altri, con alta affinità elettronica, possono dare anioni; anioni (con una o più cariche negative) e cationi (con una o più cariche positive) possono dare luogo a strutture complesse, costituite da più atomi; non solo atomi singoli, ma anche raggruppamenti di atomi possono diventare anioni (per es. SO₄^2-, NO₃^-, N₃^-, SiO₄^4- ecc.) o cationi (per es. NH₄⁺, Hg₂²⁺ ecc.).

Anioni e cationi si attraggono per interazione elettrostatica: questa interazione si chiama legame ionico.

Le forze elettrostatiche seguono la legge di Coulomb, che esprime la forza di interazione tra due corpi carichi:

k = costante (che dipende anche dalle unità usate)

Z_a, Z_b = cariche (con segno) dei due ioni che interagiscono

r_ab = distanza tra i due nuclei

Occorre notare che la legge riguarda cariche puntiformi, e gli ioni non lo sono, ma può essere considerata valida in prima approssimazione (in particolare fino a che r_ab non diventa molto piccola).

F è negativa se Z_a e Z_b hanno segno opposto; ciò corrisponde alla attrazione fra le due cariche, essendo F un vettore che ha come come direzione la stessa di r; F negativa comporta una riduzione di r_ab.

F è positiva se Z_a e Z_b hanno segno eguale (sia ambedue positivi, sia ambedue negativi): ciò corrisponde alla repulsione, con aumento di r_ab.

Poiché queste forze, attorno ad uno ione, hanno simmetria sferica (l'azione della forza si esercita in modo perfettamente uguale in tutte le direzioni) il legame ionico non è direzionale.

Inoltre ogni catione tende ad attrarre il maggior numero di anioni e viceversa, in modo da rendere massima la forza complessiva di interazione e minima l’energia.

Mano a mano che gli ioni di carica opposta si avvicinano (quando cioè r_ab diminuisce), aumentano contemporaneamente le forze di attrazione fra gli ioni ma anche quelle di repulsione fra gli elettroni esterni.

La distanza di legame è quella che si ha quando esiste un perfetto equilibrio tra le forze di attrazione e quelle di repulsione. Questa distanza viene considerata uguale alla somma dei raggi ionici dei due ioni che interagiscono. Le dimensioni dei raggi dipendono dal numero di elettroni totali dello ione e dal rapporto tra numero di elettroni e numero atomico (cioè numero di protoni nel nucleo).

Esaminiamo una tabella di ioni isoelettronici (che hanno cioè lo stesso numero di elettroni) con i relativi raggi ionici:

Fig.13.1 Raggi ionici per ioni isoelettronici. Escluso H, in forma di idruro, dato che non fa parte degli alogeni, per gli altri si può notare che il raggio diminuisce fortemente all'aumentare della carica (da sinistra a destra, il nucleo attrae sempre più gli elettroni rimastigli attorno, mano a mano che essi diminuiscono di numero) e che i raggi aumentano dall'alto verso il basso poiché aumenta il numero quantico n, corrispondente al guscio degli elettroni esterni.

Il numero di elettroni persi o acquistati si chiama valenza ionica e non può mai essere superiore a 3; non bisogna confonderlo perciò con lo stato di ossidazione, che è formale, non reale (nel calcolo dello stato di ossidazione si "suppone" che tutti gli elettroni corrispondenti passino all'atomo più elettronegativo, ma non si tratta di un processo reale, bensì di un artificio utile nei calcoli).

Gli ioni non si possono avvicinare a meno della somma dei rispettivi raggi ionici; il limite al numero di ioni di carica opposta che circondano uno ione è imposto dalla non compenetrabilità degli ioni coinvolti e dal dover essere a contatto fra loro (cosa che provoca repulsione da parte degli elettroni dei due atomi).

Date due specie A⁺ e B^- potremo avere situazioni di impaccamento diverso in funzione delle dimensioni relative di A⁺ e B^- cioè dai rispettivi r⁺ e r^-; l'impaccamento rappresenta la relativa disposizione degli ioni nello spazio (come se si trattasse di sferette rigide; in effetti le sfere sono deformate in funzione delle forze elettrostatiche di attrazione e repulsione) e viene individuato dal "numero di coordinazione" spaziale di ognuno degli ioni.

Per semplicità, nella figura successiva vengono schematizzate tre diverse situazioni di coordinazione sul piano, considerando gli ioni come sfere rigide indeformabili.

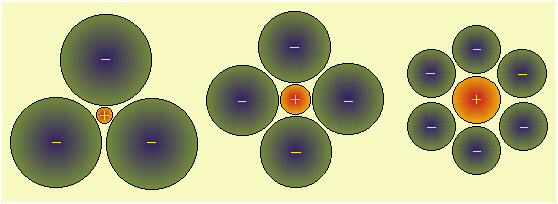
Fig.13.2 Tipi di coordinazione planare tra ioni con rapporti di raggi ionici diversi. Nel primo caso il rapporto r⁺/r^- è molto piccolo; nel secondo caso è intermedio, nel terzo è circa eguale ad 1. Nel secondo caso si può immaginare la situazione tridimensionale in cui un anione appoggia sulle 4 sfere negative sopra al piano del disegno, ed un'altra sta sotto: la simmetria è quella di un ottaedro. Come il catione è circondato da anioni, anche ogni anione è circondato da cationi., così che la carica totale sia nulla (la materia è elettricamente neutra).

Il numero di ioni che circondano il catione con carica n⁺ si chiama numero di coordinazione dello ione Aⁿ⁺.

Se consideriamo perciò gli ioni come sfere rigide (secondo il modello semplificato che usiamo), possiamo individuare i numeri di coordinazione più probabili, in funzione del rapporto r⁺/r^- tra i raggi.

Nello schema seguente sono indicati i tipi più comuni di coordinazione, con la relativa simmetria nello spazio (la trigonale è solo planare), in funzione del rapporto tra il raggio ionico del catione (che è quasi sempre più piccolo) e quello dell'anione.

Fig.13.3 Tipi di coordinazione in funzione del rapporto tra i raggi ionici

In effetti il modello delle sfere rigide non è proprio corretto: possono esserci adattamenti e deformazioni della nuvola elettronica a causa delle attrazioni-repulsioni (polarizzazione) e questo può portare a variazioni nei limiti indicati in fig.13.3.

I numeri di coordinazione indicati nella tabella non sono gli unici possibili; in sistemi complessi come nei silicati (rocce) è possibile avere comunemente anche coordinazione 12 e oltre; in questi casi i cationi sono facilmente sostituibili da altri analoghi (poiché i legami ionici parziali coinvolti sono molto deboli).

E’ importante non confondere il numero di coordinazione con il rapporto stechiometrico fra gli ioni in un sistema. Nella formula chimica di composti ionici è necessario che l’unità indicata sia elettricamente neutra (la sommatoria delle cariche negative deve essere eguale a quella delle cariche positive).

Si indicano, per convenzione, prima i cationi, poi gli anioni, dando ad ognuno di essi un coefficiente al piede che indica in che rapporto stechiometrico si trovano i vari componenti del sistema; per esempio:

NaCl, CaF₂, AlCl₃, Al₂O₃, K₂S, ...

E’ ovvio che non sia possibile sapere, in NaCl, a quale dei 6 Cl coordinati a un Na si riferisca l’espressione "NaCl"; ma sicuramente in un cristallo qualsiasi di NaCl, il rapporto fra il numero di Na⁺ e quello di Cl^- è eguale a 1; in uno di K₂S, il numero di K⁺ è due volte quello di S^--.

Per sapere perché le sostanze ioniche formino cristalli e non si limitino a costituire coppie ioniche isolate, occorre fare alcune considerazioni energetiche sui legami ionici.

L’energia di interazione ionica fra due ioni a e b è:

in cui i simboli hanno lo stesso significato che nell'espressione della forza, ma k' è una costante diversa da k.

E è negativa se Z_a e Z_b hanno segno opposto; se le due cariche si avvicinano, r_ab diminuisce, perciò aumenta il valore assoluto di E, ed essendo E negativa, il significato è che il sistema è più stabile quando le due cariche sono vicine piuttosto che quando si trovano a distanza infinita (situazione in cui convenzionalmente E = 0).

Viceversa, se le due cariche hanno segno eguale, E è positiva, perciò il valore minimo di energia si avrà quando le cariche si trovano a distanza infinita (sempre E = 0).

Questo però rende conto del fatto che due ioni di segno opposto formino una coppia ionica, ma non che si formino strutture cristalline, reticoli cristallini.

E' possibile capirlo se si prendono in considerazione tutte le possibili interazioni elettrostatiche che esistono in un reticolo ionico.

Prendiamo, come esempio, una sezione parallela ad una faccia di un cristallo di cloruro sodico:

Fig.13.4 Reticolo bidimensionale di un cristallo ionico di NaCl.     Il reticolo tridimensionale è costituito da una serie di reticoli eguali sfasati di una unità, in modo che ad ogni Na+ corrisponda un Cl-.

E' possibile calcolare l’energia di interazione fra N_A moli di ioni Na⁺ e N_A moli di ioni Cl^- in un reticolo cristallino, purché si conosca la disposizione di ogni ione rispetto agli altri.

Se considerassimo un solo catione, l'energia di interazione con un anione sarebbe quella già vista, cioè quella di una singola coppia. Le coppie però, in questo caso, sono N_A.

Ma perché queste N_A moli di coppie dovrebbero stare assieme e non ognuna per conto suo? Se non ci fosse qualche altra forma di energia in gioco il sistema avrebbe la stessa energia di N_A coppie isolate; non può essere questa la ragione per cui esiste il reticolo.

Nel reticolo, in effetti, c'è attrazione fra ogni singolo catione e ognuno degli anioni che lo circonda (4 nel reticolo planare, 6 nel tridimensionale), perciò l'energia di attrazione deve essere moltiplicata per un fattore che dipende dalla geometria del reticolo e dalla distanza r_ab tra due ioni adiacenti.

Ma contemporaneamente esiste anche repulsione fra quelli di segno uguale vicini. Occorre perciò tener conto di tutte le interazioni. L’espressione dell'energia totale U sarà perciò uno sviluppo in serie in cui il valore di ogni addendo dipende dalla carica degli ioni che interagiscono e dalla posizione che questi ioni occupano nel reticolo.

Fig.13.5 Geometria delle attrazioni e delle repulsioni in un reticolo cubico (NaCl). Nello sviluppo in serie si sommano tutte le interazioni possibili di ogni ione; uno ione interagisce negativamente (attrazione) con gli ioni di segno contrario adiacenti, cioè a distanza r (sono 4 sul piano, nel caso a; sarebbero 6 in tridimensionale); interagisce positivamente (repulsione) con ioni a distanza   r Ö2 (4 sul piano, caso b; ma sarebbero 12 in tridimensionale); interagisce ancora negativamente con ioni a distanza r Ö5 (8 solo sul piano, caso c) e così via.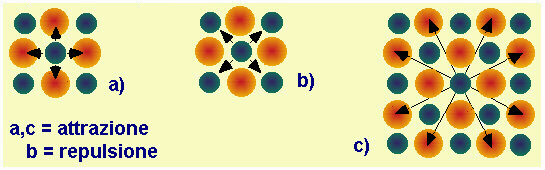

Lo sviluppo in serie, costruito semplicemente sulla base della struttura geometrica del reticolo (e indipendente perciò dagli ioni che effettivamente occupano le posizioni), è costituito da una sequenza di addendi alternativamente negativo e positivo, ma di entità sempre più piccola; esso converge verso un valore numerico che si chiama Costante di Madelung e che non dipende dal valore di r_ab, ma dall'arrangiamento geometrico del reticolo.

La costante di Madelung dipende perciò solo dal tipo di reticolo e dalla mutua posizione geometrica dei singoli ioni, non dalla loro natura.

Fig.13.6 Costanti di Madelung per vari tipi di reticolo cristallino. ZnS si può presentare con due diversi tipi di reticolo cristallino, caratterizzati da un diverso tipo di impaccamento e perciò da due diverse costanti di Madelung. Anche se gli ioni costituenti sono diversi da quelli indicati (e perciò con diversi raggi ionici), a parità di tipo di reticolo la costante di Madelung è la stessa.

La costante è sempre maggiore di uno: l’energia di attrazione elettrostatica globale è perciò maggiore nel reticolo che nel caso di una coppia discreta.

Questa energia, che si ottiene moltiplicando l'energia di interazione della coppia per la costante di Madelung relativa, con le debite correzioni, si chiama U_ret= energia reticolare, unica responsabile della stabilità dei cristalli delle sostanze ioniche. Se essa non ci fosse, esisterebbero solo coppie ioniche isolate.

U_ret corrisponde, per esempio nel caso di NaCl solido, alla energia della sua formazione a partire dagli ioni gassosi:

Na⁺_(g) + Cl^-_(g) ® NaCl_(s)

Per determinare sperimentalmente la U_ret di un composto, si può utilizzare il Ciclo di Born-Haber. Proviamo ad applicarlo al caso di NaCl. La reazione di formazione di NaCl dagli elementi nel loro stato normale (solido per Na, gassoso per Cl₂) che è indicata nel riquadro in alto, comporta una energia nota; ma per conoscere l'energia coinvolta nella reazione su indicata, occorre portare, in vari stadi semplici, Na solido a Na⁺ gassoso e Cl₂ a Cl^- gassoso:

* DE1 (formazione da elementi) -4,08 x 105 J mol-1 * DE2 (sublimazione Na solido) +1,06 x 105 J mol-1 * DE3 (rottura legame Cl2) +1,18 x 105 J mol-1 * DE4 (ionizzazione Na ) +4,94 x 105 J mol-1 * DE5 (ionizzazione Cl, affinità elettronica) -3,57 x 105 J mol-1 * Uret ( formazione reticolo cristallino ) -0,47 x 105 J mol-1 Uret  è negativa: il reticolo cristallino è più stabilizzato di 1 mole di coppie ioniche indipendenti NaCl.

Fig.13.7 Schema del Ciclo di Born-Haber per NaCl.

La reazione in alto corrisponde alla formazione di NaCl solido partendo dagli elementi nel loro stato stabile a 25°C e 1 atm.

Fig.13.8 Fritz Haber   Fritz Haber (1868-1934), fu uno dei più importanti chimici tedeschi, vinse il premio Nobel per la chimica nel 1918.   Si interessò in particolare della sintesi diretta dell'ammoniaca dagli elementi e su questo argomento ebbe vivaci discussioni con Nernst.

Nella formazione di sostanze ioniche sono molto importanti le energie di ionizzazione, poiché comportano spesa di energia; sarà possibile la formazione di ioni con più cariche se il guadagno di energia dovuto alla U_ret compensa quella spesa; non sarà possibile se la spesa di energia è troppo alta. Occorre conoscere perciò l'entità delle energie coinvolte in ionizzazioni successive dello stesso atomo.

Fig.13.9 Energie di successive ionizzazioni per alcuni atomi, espresse in kJ mol^-1. L'energia di II ionizzazione deve essere sommata alla prima per arrivare alla carica 2+. Per i metalli alcalini Li e Na, la prima ionizzazione comporta una energia enormemente inferiore alla seconda, perciò tenderanno a fermarsi alla situazione 1+. Per gli alcalino-terrosi Mg e Ca, la seconda è di poco superiore al doppio della prima, mentre la terza è molto più alta; tenderanno alla situazione 2+. Per B e Al, prima, seconda e terza ionizzazione comportano energie crescenti ma non in modo drammatico, mentre la quarta è enorme: tenderanno perciò a fermarsi allo stato 3+.

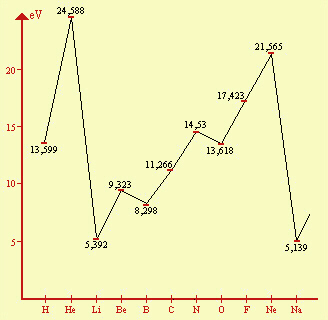
Nella figura seguente viene riportata in grafico la sequenza delle energie di I ionizzazione per gli atomi fino al primo del 3° gruppo (Na).

Fig.13.10 Energie di prima ionizzazione per gli atomi da H a Na. I valori delle energie necessarie per la ionizzazione aumentano mediamente da Li fino a Ne, per diminuire di molto nel caso di Na, simile a Li; poi l'andamento è simile, anche se con valori diversi. E' evidente una periodicità nel comportamento dei vari atomi. L'energia è espressa in elettronvolt eV: 1 eV = 1,60219x10-19 J. Per ottenere le energie di ionizzazione espresse in kJ per mole: eV x fattore di conversione x costante di Avogadro x 10-3

L'analisi delle energie di ionizzazione e dai dati di elettronegatività permette di dedurre se si formano cationi o anioni: avremo cationi da metalli con bassa energia di ionizzazione e bassa elettronegatività, anioni da non metalli con alta energia di ionizzazione e alta elettronegatività.

Poiché energie di ionizzazione ed elettronegatività sono caratteristiche periodiche, è possibile anche schematizzare, in linea di massima, che tipo di ioni è possibile ottenere nell'ambito dei vari gruppi della tavola periodica.

Fig.13.11 Tipi di ioni principali in funzione dei gruppi della tavola periodica

Nella formazione di ioni, non sempre viene raggiunta la configurazione di un gas nobile (per esempio i metalli di transizione ne sono troppo lontani), ma si raggiunge, comunque, una situazione di massima stabilità.

Esistono inoltre anche ioni poliatomici positivi, per esempio NH₄⁺, Hg₂²⁺, VO₂⁺, NO⁺, NO₂⁺...

Ma se i due tipi di atomi che sono legati fra loro non hanno una differenza di elettronegatività tanto elevata da favorire la formazione di legami ionici, in particolare, al limite, se i due atomi sono eguali, non sarà possibile il legame di tipo ionico: si formerà un legame covalente.